We know that one scientific proof for the existence of entanglement is the successful violation of Bell’s inequality. But there might still be some open questions about entanglement as such. Here is another experiment you can conduct in order to get a better feeling for it.
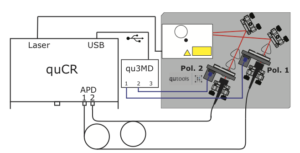
The setup is the same as in the Bell experiment (motorised version is advised, but not necessary):
Now, we keep one polariser fixed (e.g. start at horizontal polarisation) and rotate the other one, while looking at the coincidence count rates and plotting them over the angle of the rotation. The quCR software (in the motorised version) does that automatically. When the rotating polariser is back to horizontal, you change the “static” polariser to +45 degrees and so on…
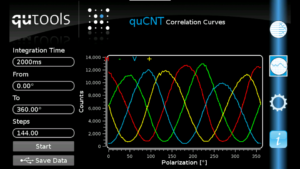
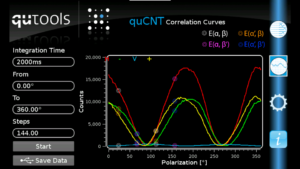
This is what you will see:
The red curve was taken with the “static” polariser set to horizontal, the green one -45 degrees, the blue one vertical and the yellow one +45 degrees.
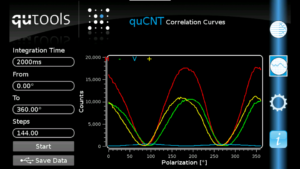
In contrast to this, a simple non-entangled state will produce the following result (wave plate in the pump beam removed):
Do you see the difference? What happens to the single count rates? Why are the correlations of the entangled photons called “non-classical”? And how is Bell’s inequality connected to these measurements?
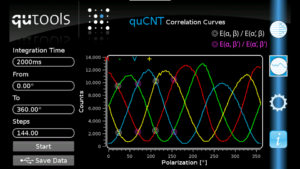
The 16 values you need to calculate Bell’s inequality (in this case the CHSH inequality) are a subset of those in the 4 curves. Here we have marked them with little circles in the first measurement result:
And in the second, too:
Why are exactly these 16 measurement positions chosen? What happens to the S value of the Bell inequality if you choose other positions?
What do you need?
- 1 x quED (motorised version advised)
Connected Experiments
- Bell’s Inequality
- Franson Interference
- QKD II: The Ekert Protocol
- QKD III: The BBM Protocol

 Interferometers
Interferometers Time-Tagger
Time-Tagger Quantum Physics Kits
Quantum Physics Kits