In quantum physics, randomness plays a big role. In non-quantum theories like classical (Newtonian) mechanics, on the other hand, everything is supposed to be deterministic. For some modern applications (for example cryptography), random numbers are important. Since there is some randomness inherent in quantum physics, why not use it to generate random numbers?

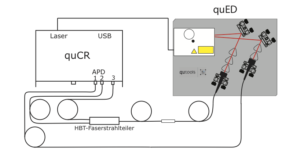
The setup is the same one as in the Hanbury Brown and Twiss experiment (particle nature of photons):

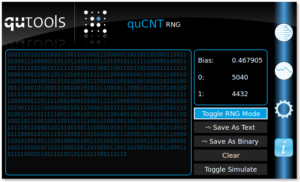
The photon detection events, however, are analysed in a different way. Usually, we count rates of detected events: singles and n-fold coincidences. Here, we only look for coincidences between detector 0 and detector 1 or 2. When detector 0 and 1 register a photon at the same time (= within the coincidence time window), we attribute a binary 0 to it, when detector 0 and 2 click simultaneously, a binary 1 is produced. By this, we create random bits:

If you also have the quED-QKD AddOn, you can even use weak coherent pulses to generate single events at the push of a button, further improving the educational value.

Now, are these good random bits? Can this be tested? What are the properties that good random number/bit generators should have?

What do you need?

• 1 x quED
• 1 x quED-HBT
• 1 x quED-QKD

Connected Experiments

• Particle Nature of Photons: Hanbury Brown & Twiss Experiment
• Quantum Cryptography/QKD: BB84